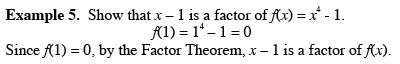QuickstartExploration p.148
Lesson(2.2) Polynomial Functions of Higher DegreeObjective: Students will know how to sketch and analyze graphs of polynomial functions.
I Graphs of Polynomial Functions
A. Characteristics
1. Polynomial functions are continuous. What this means to us is that the graphs of
polynomial functions have no breaks, holes, or gaps.
2. The graphs of polynomial functions have only nice smooth turns and bends. There are
no sharp turns as in the graph of y = |x|.
B.
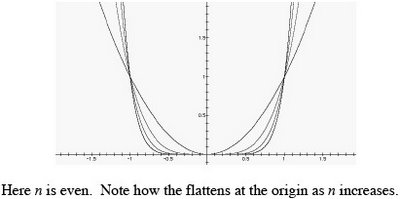
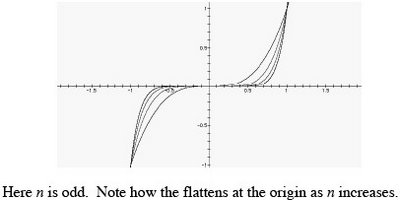
C. Polynomial Functions are transformed in the same way as we discussed for cosine and sine functions. See example 1 in the textbook. (p.148)
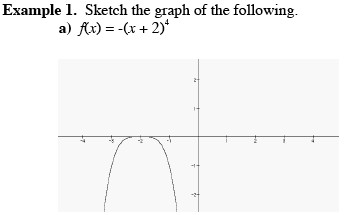
The basic function is x^4. Because a = -1 it is reflected across the x-axis. Because -2 is subtracted inside the function, the graph is translated to the left 2 units.
II Leading Coefficient Test
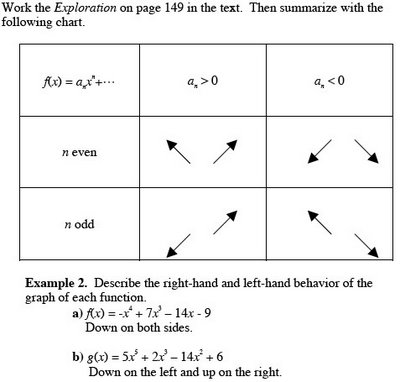
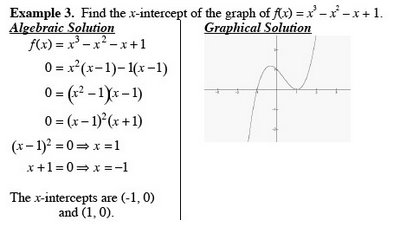
III Zeros of Polynomial Functions
The following are equivalent statements, where f is a polynomial function and a is a real number.
(p.151)1. x = a is a zero of f.
2. x = a is a solution of the equation f(x) = 0.
3. (x – a) is a factor of f(x).
4. (a, 0) is an x-intercept of the graph of f.
Complete the Exploration on p.150
Part (a) has 3 zeros and 2 extrema, (b) 4 zeros and 3 extrema, (c) 3 zeros and 2 extrema.
It can be shown that for a polynomial function f of degree n, the following statements are true.
1. The graph of f has at most n real zeros.
2. The function f has at most n - 1 relative
extrema (relative minimums or maximums).
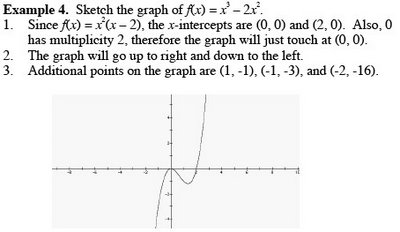
Note that in the above example, 1 is a repeated zero. In general, a factor (x – a)k, k > 1, yields a repeated zero x = a of
multiplicity k. If k is odd, the graph crosses the x-axis at x = a. If k is even, the graph only touches the x-axis at x = a.
IV. Intermediate Value Theorem
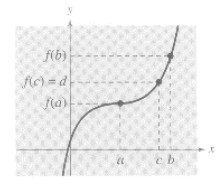
Let a and b be real numbers such that a < style="font-style: italic;">different signs.
 Homework
HomeworkWriting about Math
p. 155