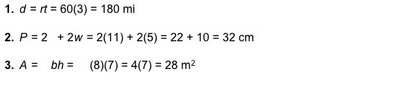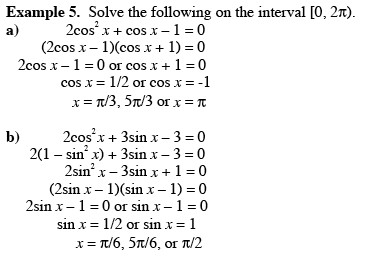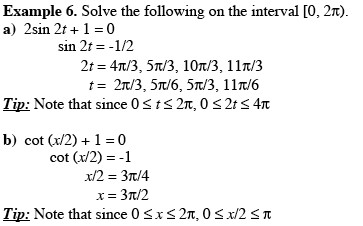Algebra I: Lesson Plan * 9/22/2006

• Quickstart Check Skills You'll Need p.111 #1 - 3Solution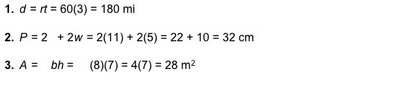
• Investigation: Using a Transformed Formula (p.111)
• Lesson
  (2-6) Formulas
  
  1. Transforming Formulas
     
  2. Transforming Equations
     
     
  3. Transforming Equations with only variables
  4. Why can't we divide by zero?
     
• Complete Posters
• Odyssey - Login with student ID for username and password
  
• Reminders
  Monday - 2-4 thru 2-6 Quiz
  Wednesday - Chapter 2 Test
  

PreCalculus: Lesson Plan * 9/22/2006

• p.403 #85 - 95 odd
• Return Chapter 4 Test and Review of Chapter 4
• Reminders
  Monday - 5.3 Quiz - Solving Trig Equations
  Wednesday - Chapter 4 ReTest - Trig Basics
  Friday - Chapter 5 Test - Trig Identities and Solving Equations
  

Algebra I: Lesson Plan * 9/21/2006

• Quickstart
  FCAT Practice
  p.110 #35 - 39
  
• Work on Posters
  

PreCalculus: Lesson Plan * 9/21/2006

• Quickstart p.389 #19, 21
• (5.2) Verifying Identities Discussion & Review
• Lesson 5.2 Quiz
  p.389 - 390 #10, 26, 28 [10 pts]
• Homework
  p.400 - 403 #3 - 42 x 3's, 57, 60
  

PreCalculus: Lesson Plan * 9/20/2006

• Quickstart p.391 #91 - 95 odd
• Lesson
  (5.3) Solving Trigonometric Equations
  Read Section 5.3
  
  
  
  complete practice problems
  p.400 - 403 #3 - 42 x 3's, 57, 60
  

Algebra I: Lesson Plan * 9/20/2006

• Quickstart Red and Blue workbook p.20
  Solving Equations with variables on Both Sides MA.A.3.4.2, MA.D.2.4.2
• Lesson
  (2-4) Solving Equations with variables on Both Sides
  Jigsaw activity
  Green Workbook p. 25 - 26 #1 - 33
  (2-5) Equations and Problem Solving
  Group Poster
  Green workbook p.27 1, 2, 3, 6, 7, 8, 9
  
  

Algebra I: Lesson Plan * 9/19/2006

• Quickstart
  Red and Blue workbook p.19
  Solving Multi-Step Problems
  MA.B.2.4.2, MA.D.1.4.2, MA.D.2.4.2
• Lesson
  (2-4) Solving Equations with Variables on Both Sides
  Green Workbook p.26 #1 - 33, one column
  

PreCalculus: Lesson Plan * 9/19/2006

• Quickstart p.383 #71, 73
• Lesson
  1. (5.2) Verifying Trigonometric Identities
     
     • Guidelines
       1. Work with only one side of the equation at a time. Usually it is better to start with the more complicated side first.
       2. Look for opportunities to factor an expression, add fractions, square a two term quantity, or create a single term denominator.
       3. Look for opportunities to use the fundamental identities. Note which functions are in the final expression you want. Sine and cosine pair well, as do secant and tangent, and cosecant and cotangents.
       4. As a last resort, convert all terms to sine and cosine.
       5. Always try something. Even paths that lead to dead ends give you insight.
  2. Real-Life Application p.391 #70
  3. Check Understanding
     (5.1) Student Success Organizer Examples 1, 2
     
  4. Chapter 1 Review
     
• Homework
  p. 389 - 391 #3 - 9 x 3's, 20, 21, 24 - 51 x 3's
  SECTION 5.2 QUIZ on THURSDAY
  

PreCalculus: Lesson Plan * 9/18/2006

• Quickstart p.307 #19, 23
• Lesson
  Chapter 5 Analytic Trigonometry
  (5.1) Using Fundamental Identities
  Section Objectives: Students will know how to use fundamental trigonometric identities to evaluate trigonometric functions and simplify trigonometric expressions.
  
  1. Introduction (p. 376)
     Review the following list of identities that we have covered so far.
     Reciprocal Identities
     sin u = 1 / csc u
     cos u = 1 / secu
     tan u = 1 / cot u
     csc u = 1 / sin u
     sec u = 1 / cosu
     cot u = 1 / tan u
     Quotient Identities
     tan u = sin u/cosu
     cot u = cos u/sin u
     Pythagorean Identities
     sin²u + cos²u = 1
     tan²u + 1 = sec²u
     1 + cot²u = csc²u .
     Cofunctions Identities
     sin (90° - u) = cos u
     tan (90° - u) = cot u
     sec (90° - u) = csc u
     cos (90° - u) = sin u
     cot (90° - u) = tan u
     csc (90° - u) = sec u
     Even/Odd Identities
     sin (-u) = - sin u
     cos (-u) = cos u
     tan (-u) = - tan u
     cot (-u) = - cot u
     sec (-u) = sec u
     csc (-u) = - csc u
     
  2. Using the Fundamental Identities (pp 377 - 380)
     
     • Example 1. If csc u = -5/3 and cos u > 0, find the values of the other five trigonometric functions.
       sin u = -3/5
       cos²u = 1- sin²u = 1- (-3/5)² = 16/25
       cos u = 4/5
       sec u = 5/4
       tan u = sin u/cosu = (-3/5) / (4/5) = -3/4
       cot u = -4/3
     • Example 2. Simplify the following
     1. csc²x cot x – cot x
        = (csc² x – 1)cot x = (cot² x)cot x = cot³x
     2. tan x sin x + cos x
        = (sin x / cos x)sin x + cos x
        = (sin²x/cosx) + cosx
        = (sin²x/cosx) + (cos²x/cosx)
        = (sin²x + cos²x)/cos x
        = 1/cos x
        = sec x
     3. (sec t/tan t) - (tant/1+ sec t)
        = [sec t(1+ sec t)- tan²t]/[tant(1+ sec t)]
        = [sec t + sec²t - tan²t]/tan t(1+ sec t)
        = (sec t + 1)/[tant(1 + sec t)]
        = 1/tan t
        = cot t
        
     • Example 3. Factor the following trigonometric expressions
     1. cos²x – 1
        = (cos x + 1)(cos x – 1)
        b) sin²u – 3sin u – 10
        = (sin u + 2)(sin u – 5)
        c) sec²t – tan t – 3
        = (tan²t + 1) – tan t – 3
        = tan²t – tan t – 2
        = (tan t + 1)(tan t – 2)
        
     • Example 4. Rewrite 1/(sec x -1) so that it is not a fraction.
       1/(sec x -1) = [1/(sec x -1)] × [(sec x + 1)/(sec x + 1)]
       = (sec x + 1)/(sec² x - 1)
       = (sec x +1)/tan ²x
       = (sec x/tan² x) + (1/tan²x)
       = [(1/cosx)(1/tanx)(1/tanx)] + (1/tan²x)
       = [(1/cosx)(cosx/sinx)(1/tanx)] + (1/tan²x)
       = [(1/sinx)(1/tanx)] + (1/tan²x)
       = cot x csc x + cot²x
       
     • Example 5. Use the substitution x = 3sin u, 0 < u < p/2,
       to express √(9 - x²) as a function of u.
       √(9 - x²)
       = √(9 -(3sin u)²)
       = √(9 - 9sin² u)
       = 3 √(1- sin² u)
       = 3 √(cos² u)
       = 3cosu
       
• Homework p.381 - 383 #1 - 70 x 3's (Due Thursday)
  

Algebra I: Lesson Plan * 9/18/2006

• Quickstart
  Investigation: Using a Table to Solve an Equation (p.96)
  
• Lesson
  (2-4) Solving Equations with Variables on Both Sides (p. 96)
  Example 1, Check Understanding 1
  Identities and Equations with No Solutions
  Example 3, Check Understanding 3
  Guided Practice p.99 #22 - 27
  (2-5) Equations and Problem Solving
  Distance - Rate - Time Problems
  Example 3
  
• Homework:
  get a good night's sleep for BAT testing
  

RCC: 9/18 - 9/22

Reading Comprehension Check #6
Complete a Cause and Effect diagram for your novel.

Instructional Focus: 9/18 - 9/22

Instructional Focus
MA.E.1.4.2 Student will be able to calculate measures of central tendency (mean, median, mode, and dispersion (range, standard deviation, and variance) for complex sets of data and determines the most meaningful measure to describe the data.